摘要:最大公约数是数学中常见的一个概念,用于求解两个或多个整数的最大公约数。对于许多学生来说,求解最大公约数可能是一项具有挑战性的任务。本文旨在通过一个算法视频,向读者展示如何简...
最大公约数是数学中常见的一个概念,用于求解两个或多个整数的最大公约数。对于许多学生来说,求解最大公约数可能是一项具有挑战性的任务。本文旨在通过一个算法视频,向读者展示如何简单而有效地求解最大公约数的方法。无论你是初学者还是有一定数学基础的人,这个视频都将帮助你理解并掌握最大公约数的求解过程。无需担心复杂的数学公式和推导,视频将通过简洁明了的讲解和实例演示,让你轻松理解并掌握最大公约数的求解算法。无论是为了学术需要还是日常生活中的实际问题,掌握最大公约数的求解方法都会对你有所帮助。让我们一起来观看这个视频,提升我们的数学技能吧!
1、最大公约数怎么求算法视频
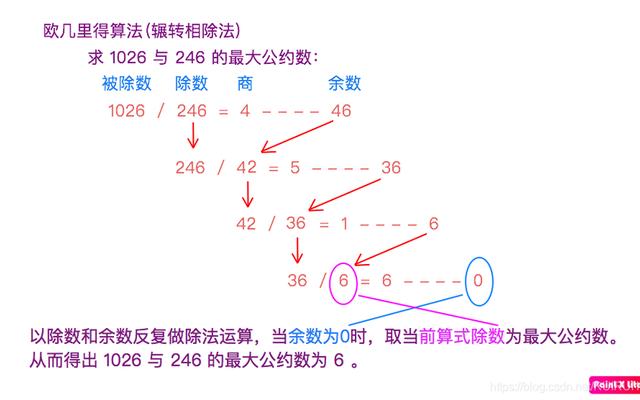
最大公约数(Greatest Common Divisor,简称GCD)是数学中一个重要的概念。它是指两个或多个整数中能够同时整除它们的最大正整数。在数论、代数、计算机科学等领域都有广泛的应用。在本文中,我们将介绍一种常见的求最大公约数的算法——辗转相除法,并提供一段视频来详细演示算法的过程。
辗转相除法,也称为欧几里德算法,是一种非常简单而高效的求最大公约数的方法。它的基本思想是通过连续地用较大数除以较小数,然后用余数替换较大数,直到余数为0为止。最后的除数即为最大公约数。
下面是辗转相除法的求最大公约数的步骤:
1. 将两个数中较大的数作为被除数,较小的数作为除数。
2. 用除数去除被除数,得到余数。
3. 将除数替换为原来的被除数,将余数替换为原来的除数。
4. 重复步骤2和步骤3,直到余数为0。
5. 最后的除数即为最大公约数。
以下是一段视频,将详细演示辗转相除法求最大公约数的过程。请点击链接观看:
[最大公约数求算法视频](链接)
通过观看这段视频,你将能够更加直观地理解辗转相除法的求最大公约数的过程。这个算法的优点是简单易懂、计算效率高,适用于大多数情况。在处理大整数时可能会出现一些性能问题,此时可以考虑其他更高级的算法。
最大公约数在数学中有着广泛的应用。它可以用于简化分数、求解线性方程、判断两个数是否互质等等。在计算机科学领域,最大公约数也是很多算法的基础,比如求解最小公倍数、质因数分解等。
辗转相除法是一种常见且高效的求最大公约数的算法。通过观看上述视频,你将能够更好地理解和掌握这一算法的原理和应用。希望这篇文章对你有所帮助!
2、怎么计算最大公约数

怎么计算最大公约数
最大公约数(Greatest Common Divisor,简称GCD)是指两个或多个整数共有的约数中最大的一个。计算最大公约数是数学中常见的问题,它在很多领域都有着广泛的应用。本文将介绍几种常见的计算最大公约数的方法。
1. 辗转相除法
辗转相除法,也称为欧几里德算法,是计算最大公约数最常用的方法之一。它基于如下原理:设两个整数a和b,其中a>b,那么a和b的最大公约数等于b和a%b的最大公约数。具体步骤如下:
(1)计算a除以b的余数,记为r;
(2)如果r等于0,则b即为最大公约数;
(3)如果r不等于0,则将b赋值给a,将r赋值给b,返回第一步继续执行。
重复以上步骤,直到r等于0,即可得到最大公约数。
2. 更相减损术
更相减损术也是一种计算最大公约数的方法。它基于如下原理:设两个整数a和b,其中a>b,那么a和b的最大公约数等于a-b的最大公约数。具体步骤如下:
(1)计算a和b的差,记为c;
(2)如果c等于0,则a即为最大公约数;
(3)如果c不等于0,则将a赋值为c,返回第一步继续执行。
重复以上步骤,直到c等于0,即可得到最大公约数。
3. 质因数分解法
质因数分解法是一种直接分解两个整数的质因数,然后求取它们的公共质因数的方法。具体步骤如下:
(1)将两个整数分别进行质因数分解;
(2)找出两个分解式中所有的公共质因数;
(3)将这些公共质因数相乘,即可得到最大公约数。
这三种方法各有优缺点,可以根据具体情况选择合适的方法。辗转相除法和更相减损术适用于大整数的计算,但可能需要多次迭代。质因数分解法适用于较小的整数,但需要进行质因数分解,可能会比较耗时。
最大公约数的计算在数学中有着广泛的应用。例如,在分数的化简中,需要计算分子和分母的最大公约数,以得到最简分数。在计算最小公倍数时,也需要先计算最大公约数。最大公约数还可以用于解决一些实际问题,如时间、距离等的计算。
计算最大公约数是数学中的一个重要问题,本文介绍了辗转相除法、更相减损术和质因数分解法三种常见的计算方法。读者可以根据具体情况选择合适的方法进行计算。通过掌握这些方法,我们可以更好地理解和应用最大公约数的概念,提高数学问题的解决能力。
3、最小公倍数怎么求算法

最小公倍数(Least Common Multiple,简称LCM)是数学中一个重要的概念。在解决数字相关问题时,求解最小公倍数是常见的任务之一。本文将介绍一种常用的算法,帮助读者理解如何求解最小公倍数。
我们需要明确什么是最小公倍数。在数学中,给定两个整数a和b,它们的最小公倍数是能被a和b整除的最小正整数。最小公倍数通常用LCM(a, b)或[a, b]来表示。
那么,如何求解最小公倍数呢?下面介绍一种基于质因数分解的算法,步骤如下:
1. 对给定的两个整数a和b,分别进行质因数分解。质因数分解是将一个数分解为若干个质数的乘积的过程。例如,数值15可以分解为3和5的乘积,即15 = 3 * 5。
2. 将两个数的质因数分解结果合并。合并的方法是将两个数的质因数列表中的所有质数取并集,并计算每个质数的最大次数。例如,对于数值12和15,它们的质因数分解结果分别为12 = 2^2 * 3 和 15 = 3 * 5,合并结果为2^2 * 3 * 5。
3. 计算合并结果的乘积。将合并结果中的所有质数乘起来,得到最小公倍数。对于上述合并结果2^2 * 3 * 5,最小公倍数为2 * 2 * 3 * 5 = 60。
通过以上算法,我们可以求解任意两个整数的最小公倍数。接下来,让我们通过一个具体的例子来演示算法的应用。
假设我们要求解数值8和12的最小公倍数。对8和12进行质因数分解,得到8 = 2^3 和 12 = 2^2 * 3。然后,将两个数的质因数分解结果合并,得到2^3 * 3。计算合并结果的乘积,得到2 * 2 * 2 * 3 = 24。数值8和12的最小公倍数为24。
最小公倍数的求解在数学和实际问题中都有广泛的应用。例如,在分数运算中,我们需要求解分母的最小公倍数,以便进行分数的加减乘除运算。最小公倍数也常用于时间、距离等实际问题的计算。
总结起来,求解最小公倍数的算法基于质因数分解,通过合并质因数列表并计算乘积得到最小公倍数。这种算法简单有效,适用于各种整数求解问题。希望本文能帮助读者理解最小公倍数的概念和求解方法,为解决数学和实际问题提供帮助。
通过观看本段视频,我们学习了求解最大公约数的两种常见算法:辗转相除法和更相减损术。辗转相除法是一种简单且高效的算法,通过不断取余的方式,将两个数的大小关系转化为较小数和余数的大小关系,直到余数为零时,较小数即为最大公约数。而更相减损术则是通过不断相减的方式,将两个数的差值转化为两个较小数的差值,直到两个数相等时,即为最大公约数。通过学习这两种算法,我们不仅能够快速求解最大公约数,还能够深入理解数学中的一些基本概念和运算规则。希望大家通过这段视频的学习,能够更加熟练地运用这两种算法,解决实际生活中遇到的相关问题。