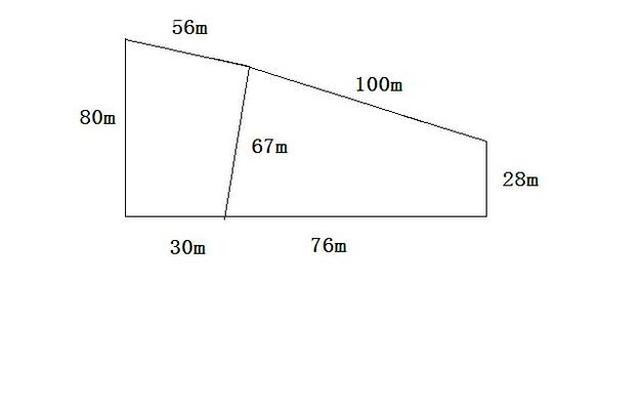
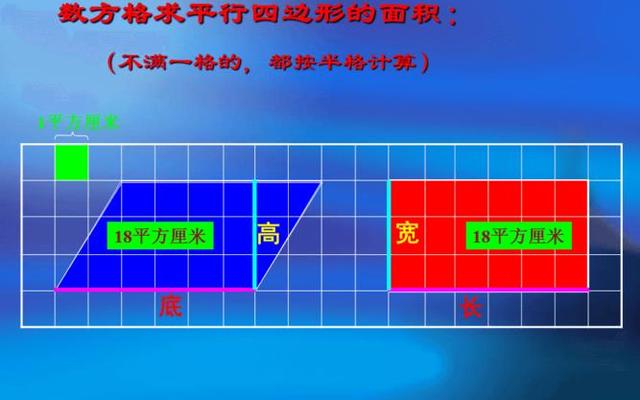
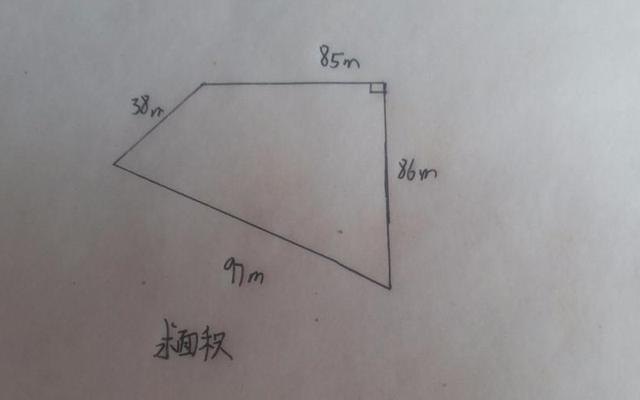
摘要:不规则四边形是一种具有不同边长和不同内角的多边形,计算其面积一直是数学中的难题。本文将介绍一种通用的不规则四边形计算面积的公式,并通过实例演示其应用。通过掌握这个公式,我们...
不规则四边形是一种具有不同边长和不同内角的多边形,计算其面积一直是数学中的难题。本文将介绍一种通用的不规则四边形计算面积的公式,并通过实例演示其应用。通过掌握这个公式,我们可以更准确地计算不规则四边形的面积,为解决实际问题提供便利。
1、不规则四边形计算面积公式
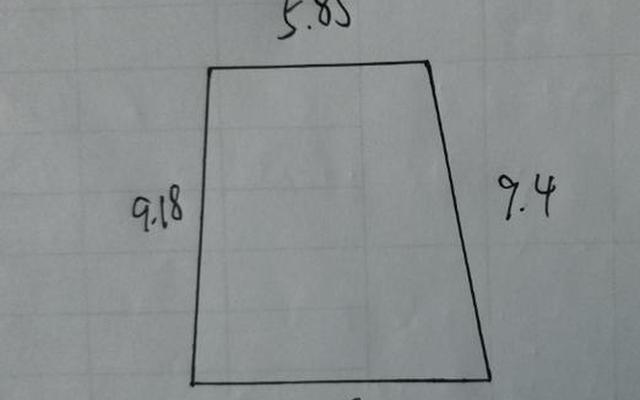
不规则四边形是指四边形的边长和角度都不相等的一种几何形状。与矩形、正方形等规则四边形不同,不规则四边形的面积计算相对复杂一些。本文将介绍不规则四边形的面积计算公式,并通过实例进行说明。
计算不规则四边形的面积需要根据其特点选择合适的方法。一般情况下,我们可以将不规则四边形分割成两个三角形或四个三角形,然后计算每个三角形的面积,最后将各个三角形的面积相加得到不规则四边形的总面积。
方法一:将不规则四边形分割成两个三角形
我们需要测量不规则四边形的两条对角线的长度。假设不规则四边形的对角线长度分别为d1和d2。然后,我们可以使用以下公式计算每个三角形的面积:
S1 = 0.5 * d1 * h1
S2 = 0.5 * d2 * h2
其中,h1和h2分别代表两个三角形的高度。将两个三角形的面积相加得到不规则四边形的总面积:
S = S1 + S2
方法二:将不规则四边形分割成四个三角形
与方法一类似,我们需要测量不规则四边形的两条对角线的长度。假设不规则四边形的对角线长度分别为d1和d2。然后,我们可以使用以下公式计算每个三角形的面积:
S1 = 0.5 * d1 * h1
S2 = 0.5 * d2 * h2
S3 = 0.5 * d1 * h3
S4 = 0.5 * d2 * h4
其中,h1、h2、h3和h4分别代表四个三角形的高度。将四个三角形的面积相加得到不规则四边形的总面积:
S = S1 + S2 + S3 + S4
下面,我们通过一个实例来具体说明不规则四边形的面积计算方法。假设有一个不规则四边形,其对角线长度分别为d1 = 6 cm和d2 = 8 cm,分割成两个三角形。三角形1的高度为h1 = 4 cm,三角形2的高度为h2 = 3 cm。根据方法一,我们可以计算出每个三角形的面积:
S1 = 0.5 * 6 cm * 4 cm = 12 cm²
S2 = 0.5 * 8 cm * 3 cm = 12 cm²
将两个三角形的面积相加得到不规则四边形的总面积:
S = 12 cm² + 12 cm² = 24 cm²
通过以上实例,我们可以看出,不规则四边形的面积计算方法相对简单,只需要测量对角线长度和各个三角形的高度,然后套用相应的公式即可。如果不规则四边形的形状更加复杂,可以将其分割成更多的三角形进行计算。
总结起来,不规则四边形的面积计算公式主要有两种方法:分割成两个三角形或四个三角形。通过测量对角线长度和各个三角形的高度,可以计算出每个三角形的面积,最后将各个三角形的面积相加得到不规则四边形的总面积。这些方法可以在实际应用中帮助我们准确计算不规则四边形的面积。
2、不规则四边形计算面积对角线
不规则四边形是指四边形的四条边长和四个内角均不相等的几何图形。在数学中,计算不规则四边形的面积和对角线长度是一项基本的几何问题。本文将以此为主题,介绍如何计算不规则四边形的面积和对角线长度。
我们来讨论如何计算不规则四边形的面积。对于任意一个不规则四边形,我们可以将其划分为两个三角形或四个三角形,并分别计算每个三角形的面积,最后将它们相加得到整个不规则四边形的面积。
对于一个三角形,我们可以使用海伦公式或正弦定理来计算其面积。海伦公式是指通过三角形的三条边长来计算其面积的公式,公式为:
面积 = √(s(s-a)(s-b)(s-c))
其中,s为三角形的半周长,a、b、c为三角形的三条边长。而正弦定理是指通过三角形的一个角和与其对应的两条边的关系来计算其面积的公式,公式为:
面积 = 0.5 * a * b * sin(C)
其中,a、b为三角形的两条边长,C为夹角。
对于不规则四边形,我们可以将其划分为两个三角形,然后分别计算每个三角形的面积,最后将它们相加得到不规则四边形的面积。
接下来,我们来讨论如何计算不规则四边形的对角线长度。对于一个不规则四边形,它有两条对角线,分别连接了相邻的两个顶点。我们可以使用勾股定理来计算不规则四边形的对角线长度。
勾股定理是指直角三角形中,直角边的平方等于两个直角边的平方和。对于一个不规则四边形的对角线,我们可以将其划分为两个直角三角形,然后分别计算每个直角三角形的对角线长度,最后将它们相加得到不规则四边形的对角线长度。
总结一下,计算不规则四边形的面积和对角线长度是一项基本的几何问题。对于面积的计算,我们可以将不规则四边形划分为若干个三角形,然后分别计算每个三角形的面积,最后将它们相加。对于对角线长度的计算,我们可以使用勾股定理将不规则四边形的对角线划分为若干个直角三角形,然后分别计算每个直角三角形的对角线长度,最后将它们相加。
通过以上方法,我们可以准确地计算不规则四边形的面积和对角线长度。这项几何问题在实际生活中有着广泛的应用,例如在建筑设计、地理测量等领域都需要对不规则四边形进行面积和对角线长度的计算。希望本文能够对读者理解和应用不规则四边形的面积和对角线长度有所帮助。
3、不规则四边形的面积计算

不规则四边形是一种几何形状,它的四个边长和四个角度都可以不相等。由于不规则四边形的形状复杂,因此计算其面积相对较为困难。我们可以利用一些数学方法来求解不规则四边形的面积。
对于不规则四边形,我们可以将其分割成两个三角形或者两个梯形,然后分别计算它们的面积,最后将两个部分的面积相加即可得到整个不规则四边形的面积。
我们可以通过海伦公式来计算三角形的面积。海伦公式是一个用于计算三角形面积的公式,它的形式为:
面积 = √(s(s-a)(s-b)(s-c))
其中,s是三角形的半周长,a、b、c分别是三角形的三个边长。
对于不规则四边形,我们可以将其分割成两个三角形。假设不规则四边形的四个顶点依次为A、B、C、D,我们可以选择将其分割成三角形ABC和三角形ACD。然后,我们可以分别计算这两个三角形的面积。
在计算三角形ABC的面积时,我们需要知道三边的长度。可以通过计算点A和点C之间的距离,以及点B和点C之间的距离来得到这些长度。
同样地,在计算三角形ACD的面积时,我们需要知道三边的长度。这可以通过计算点A和点C之间的距离,以及点C和点D之间的距离来得到。
通过海伦公式,我们可以分别计算出三角形ABC和三角形ACD的面积。然后,将这两个面积相加,即可得到不规则四边形的面积。
除了将不规则四边形分割成三角形,我们还可以将其分割成两个梯形。梯形是一个具有两个平行边的四边形。我们可以选择将不规则四边形的两条对边平行的边作为梯形的上底和下底。
我们可以通过计算梯形的上底、下底和高来求解其面积。对于不规则四边形,我们可以计算两个梯形的面积,然后将其相加,即可得到不规则四边形的面积。
总结起来,计算不规则四边形的面积可以通过将其分割成三角形或者梯形来进行。无论是使用海伦公式计算三角形的面积,还是使用梯形的面积公式计算梯形的面积,最后都需要将各个部分的面积相加,才能得到整个不规则四边形的面积。
不规则四边形的面积计算是一项基础的几何运算,它在实际生活中有着广泛的应用。无论是建筑设计、土地测量还是图像处理等领域,都需要对不规则四边形的面积进行准确的计算。掌握不规则四边形的面积计算方法对于我们来说是非常重要的。
总结全文:通过本文我们了解了不规则四边形的面积计算公式。不规则四边形是指四边形的边长和角度均不相等的图形。我们介绍了两种计算不规则四边形面积的方法:分割法和海伦公式。分割法是将不规则四边形分割成多个简单的几何形状,计算每个形状的面积然后相加。海伦公式是通过四边形的四条边长和对角线的长度来计算面积。这两种方法都需要准确测量不规则四边形的边长和角度,因此在实际应用中需要注意测量的准确性。通过学习不规则四边形的面积计算公式,我们可以更好地理解和应用几何学知识。