摘要:二次方程是数学中的重要概念,求解二次方程的对称轴公式更是解题的关键。它不仅能帮助我们找到二次函数图像的对称轴,还能进一步推导出函数的顶点坐标。通过掌握这一公式,我们能够更加...
二次方程是数学中的重要概念,求解二次方程的对称轴公式更是解题的关键。它不仅能帮助我们找到二次函数图像的对称轴,还能进一步推导出函数的顶点坐标。通过掌握这一公式,我们能够更加深入地理解二次函数的性质和变化规律,为解决实际问题提供了有力的工具。无论是在学术研究中还是在日常生活中,掌握二次方程求对称轴的公式都具有重要意义。
1、二次方程求对称轴的公式
二次方程是数学中非常重要的一个概念,它在代数学和几何学中有着广泛的应用。在解析几何中,我们经常需要求解二次方程的对称轴,这个公式可以帮助我们快速而准确地求得对称轴的位置。
让我们回顾一下二次方程的一般形式:ax^2 + bx + c = 0。其中,a、b、c是已知的实数,且a不等于0。对称轴是二次曲线的一个重要特征,它是曲线上所有点关于对称轴对称的轴线。
要求解二次方程的对称轴,我们可以利用一条简单的公式:x = -b / (2a)。这个公式告诉我们,对称轴的x坐标等于二次方程中一次项系数的相反数除以二次项系数的两倍。
为了更好地理解这个公式,让我们来看一个具体的例子。假设我们有一个二次方程:2x^2 + 4x + 1 = 0。根据公式,我们可以计算出对称轴的x坐标为:x = -4 / (2 * 2) = -1。对称轴的x坐标为-1。
通过这个例子,我们可以看到,利用二次方程求对称轴的公式可以帮助我们快速地确定对称轴的位置。这个公式的推导过程可以通过解二次方程的方法得到,但是为了简化计算,我们可以直接使用这个公式来求解。
除了求对称轴的公式,二次方程还有很多其他重要的性质和应用。例如,通过求解二次方程的根,我们可以确定二次曲线与x轴的交点,从而得到曲线的图像。二次方程还与抛物线的开口方向、顶点坐标等有密切关系。
总结一下,二次方程求对称轴的公式为x = -b / (2a),它可以帮助我们快速而准确地求解二次方程的对称轴。对称轴是二次曲线的一个重要特征,它能够帮助我们更好地理解和分析二次方程的性质。希望通过本文的介绍,读者能够对二次方程的对称轴有更深入的了解。
2、求二次函数对称轴的公式
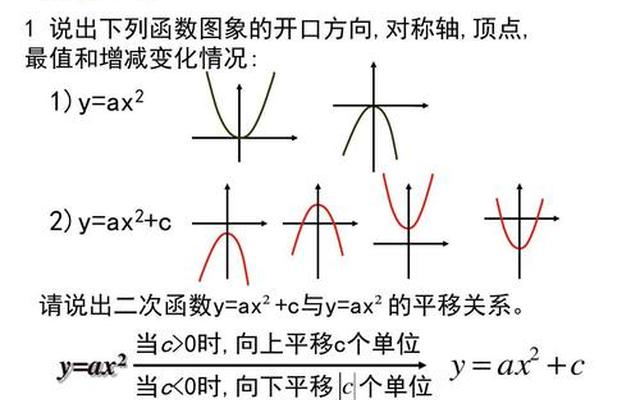
二次函数是高中数学中的重要概念,它的图像是一个抛物线。对称轴是抛物线的一个重要特征,它是指抛物线的对称中心线。在本文中,我将为大家介绍二次函数对称轴的公式。
我们来回顾一下二次函数的一般形式:y = ax^2 + bx + c。其中,a、b、c是常数,且a不等于0。二次函数的图像是一个开口向上或向下的抛物线。
对称轴是抛物线的一个特殊直线,它将抛物线分成两个对称的部分。对称轴与抛物线的每一个点都关于对称轴对称。那么,如何求二次函数的对称轴呢?
二次函数的对称轴可以通过以下公式来求解:x = -b / (2a)。
我们来看一个例子,假设有一个二次函数y = 2x^2 + 4x + 1。我们可以通过公式x = -b / (2a)来求解对称轴的x坐标。
根据公式,我们可以得到x = -4 / (2 * 2) = -4 / 4 = -1。对称轴的x坐标为-1。
现在,我们已经知道了对称轴的x坐标,那么如何确定对称轴的方程呢?其实很简单,对称轴的方程就是x = -1。
对称轴的方程是一个垂直于x轴的直线,其x坐标恒定为-1。对称轴将抛物线分成两个对称的部分,每个点关于对称轴对称。
通过对称轴的方程,我们可以判断抛物线的开口方向。如果a大于0,则抛物线开口向上;如果a小于0,则抛物线开口向下。
除了使用公式x = -b / (2a)来求解对称轴,我们还可以通过观察二次函数的系数来确定对称轴的位置。
对于一般形式的二次函数y = ax^2 + bx + c,对称轴的x坐标为-x / (2a)。我们可以发现,对称轴的x坐标与系数b的符号相反,并除以2a。
通过这个方法,我们可以更快地求解对称轴的位置,而无需进行繁琐的计算。
总结起来,二次函数的对称轴是抛物线的一个重要特征,它是抛物线的对称中心线。对称轴的公式为x = -b / (2a),其中a、b、c是二次函数的系数。
通过对称轴的方程,我们可以确定抛物线的开口方向,并判断抛物线的性质。我们还可以通过观察系数的符号来快速确定对称轴的位置。
对称轴是二次函数图像的重要特征之一,它在数学中有着广泛的应用。希望通过本文的介绍,能够帮助大家更好地理解和应用二次函数的对称轴。
3、二次函数对称轴方程公式

二次函数是数学中的一个重要概念,它在许多实际问题的建模和解决中起着重要的作用。而二次函数的对称轴方程公式是研究二次函数性质的重要工具之一。本文将以“二次函数对称轴方程公式”为主题,详细介绍其定义、性质以及应用。
我们来看一下什么是二次函数。二次函数是指形如y = ax^2 + bx + c的函数,其中a、b、c为常数,且a不等于零。二次函数的图像通常是一个开口向上或向下的抛物线。对于二次函数而言,其中一个重要的性质就是它的对称轴。
对称轴是指二次函数图像的对称中线,也可以理解为抛物线的轴线。对称轴方程公式可以用来求解二次函数的对称轴。对于二次函数y = ax^2 + bx + c,它的对称轴方程公式可以表示为x = -b / (2a)。这个公式告诉我们,二次函数的对称轴的x坐标为-b / (2a)。
接下来,我们来看一下二次函数对称轴方程公式的性质。对称轴是二次函数图像的一个重要特征,它将抛物线分成两个对称的部分。对称轴方程公式的推导基于二次函数的特性,可以通过求导或配方法得出。对称轴方程公式的应用非常广泛,可以用于求解二次函数的对称轴、顶点坐标以及其他相关性质。
在实际应用中,二次函数对称轴方程公式有着重要的作用。例如,在物理学中,二次函数可以用来描述物体的抛射运动,而对称轴方程公式可以帮助我们确定抛物线的对称轴,从而更好地理解和分析物体的运动轨迹。在经济学中,二次函数可以用来描述某些经济现象的变化规律,而对称轴方程公式可以帮助我们找到经济变量的最优值,从而指导决策和优化。
总结起来,二次函数对称轴方程公式是研究二次函数性质的重要工具,它可以帮助我们确定二次函数的对称轴,进而理解和分析二次函数的图像特点。对称轴方程公式的应用广泛,涉及到物理学、经济学等多个领域。通过深入研究和应用二次函数对称轴方程公式,我们可以更好地理解和应用二次函数的性质,为实际问题的解决提供有力支持。
通过本文的介绍,我们了解到了二次方程求对称轴的公式。对称轴是二次函数图像的一条重要线,它将图像分为两个对称的部分。根据公式x = -b/2a,我们可以轻松地求得二次函数的对称轴的x坐标。这个公式的推导过程并不复杂,只需要将二次函数的一般形式代入,并利用一些基本的代数运算即可得到结果。通过求对称轴,我们能够更好地理解二次函数图像的特点,进而解决与二次函数相关的问题。对称轴的求解不仅在数学学科中有着重要的应用,而且在其他学科中也有着广泛的应用,如物理学、工程学等。掌握二次方程求对称轴的公式对我们的学习和工作都具有重要意义。通过学习本文所介绍的公式和方法,我们可以更加灵活地运用数学知识,解决实际问题,提高自己的数学素养。


